Splitter
This BeamLab demo shows a propagation model consisting of a straight waveguide section followed by a multicore waveguide section that breaks out the single core to a two-ring multicore structure consisting of four inner cores regularly arranged on a circle of radius 17 um and 4 outer cores regularly arranged on a circle of radius 20*sqrt(2) um but rotated by 45 degrees.
BeamLab demo: splitter.m
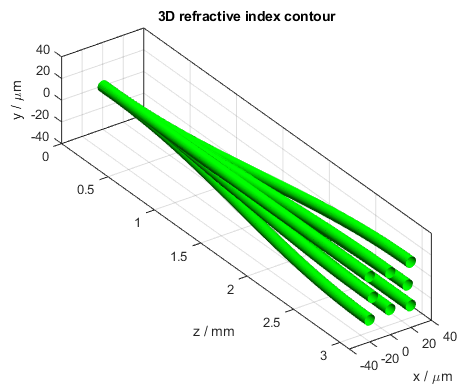
3D refractive index contour of the waveguide splitter
The following video shows how the intensity distribution changes along the propagation distance z. The left and right figures show the three-dimensional and two-dimensional intensity distribution I(x,y), respectively. Both distributions are normalized to the input intensity and displayed on a logarithmic scale from -20 dB to 0 dB.
Video of 3D (left) and 2D (right) intensity profiles
After the calculation has finished, the intensity distribution as a function of propagation distance z is plotted. The following figure depicts the intensity distribution I(x,z) at y = 0 µm. The white lines indicate the locations of the waveguides.
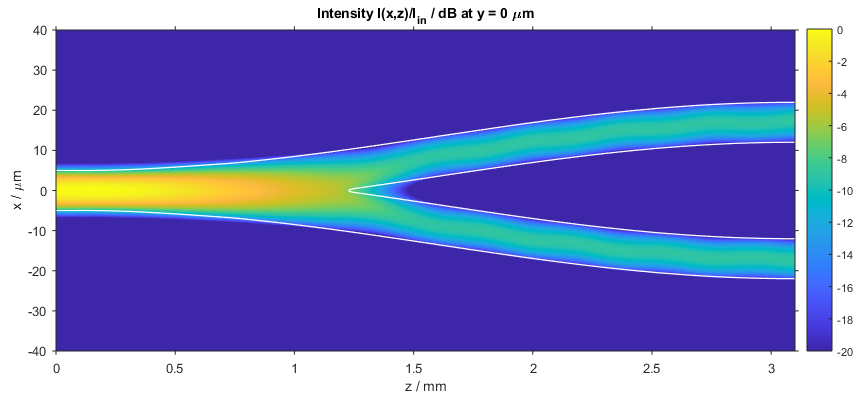
Intensity distribution in the waveguide splitter (x–z slice)
The following figure shows a compact three-dimensional view of stacked plots, each portraying the intensity distribution I(x,y) at different distances z.
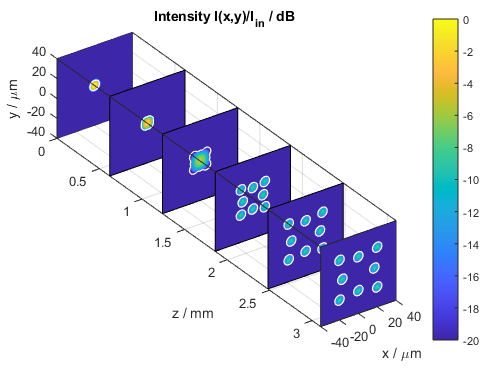
Intensity distribution in the waveguide splitter (stacked x–y slices)
Finally, the power in each core can also be independently traced during a calculation. In the figure below, the red, blue, and yellow curve represent the power of the three waveguides whose centers are located in the first quadrant of the calculation area. The power is calculated over a circular area with a 50% larger width than the core. Note that due to the symmetry conditions assumed for this example the intensity distribution in the first quadrant is, besides a rotation in the x-y plane, the same for all other quadrants and thus the power splitting ratio of this special splitter is nearly equal for all 8 output cores.
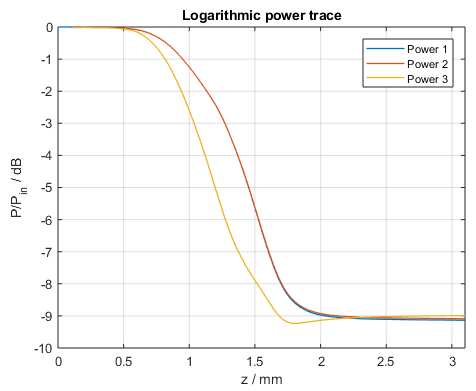
Power in each waveguide core located in the first quadrant of the calculation area
About BeamLab
BeamLab is an award-winning set of simulation tools for beam propagation through optical devices and waveguides in your familiar MATLAB® environment. It offers a high flexibility in waveguide design and post-processing of any output data.

